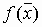 . Поэтому при поиске минимума
. Поэтому при поиске минимума 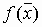 , следует
двигаться в направлении противоположном направлению градиента
, следует
двигаться в направлении противоположном направлению градиента 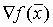 в данной точке, то есть в направлении наискорейшего спуска.
в данной точке, то есть в направлении наискорейшего спуска.
К методам первого порядка относятся алгоритмы, в которых в процессе поиска кроме информации о самой функции используется информация о производных первого порядка. К группе таких методов относятся различные градиентные методы.
Градиент функции в любой точке показывает направление наибольшего локального увеличения
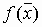 . Поэтому при поиске минимума
. Поэтому при поиске минимума 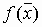 , следует
двигаться в направлении противоположном направлению градиента
, следует
двигаться в направлении противоположном направлению градиента 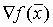 в данной точке, то есть в направлении наискорейшего спуска.
в данной точке, то есть в направлении наискорейшего спуска.
Итерационная формула процесса наискорейшего спуска имеет вид
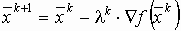 , или
, или 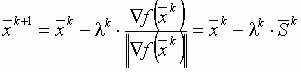 .
.
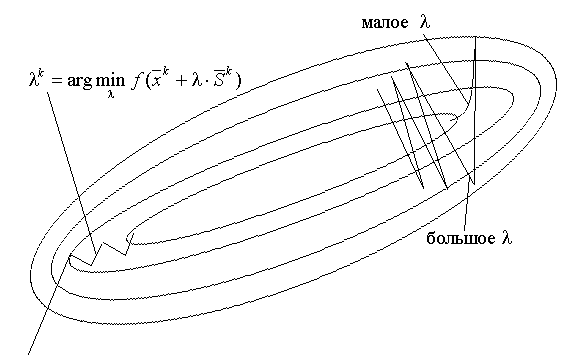
Очевидно, что в зависимости от выбора параметра λ траектории спуска
будут существенно различаться. При большом значении λ траектория спуска
будет представлять собой колебательный процесс, а при слишком больших λ
процесс может расходиться. При выборе малых λ траектория спуска будет
плавной, но и процесс будет сходиться очень медленно. Обычно λ выбирают
из условия 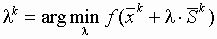 , решая одномерную задачу минимизации с использованием
некоторого одномерного метода. В этом случае получаем алгоритм наискорейшего спуска.
, решая одномерную задачу минимизации с использованием
некоторого одномерного метода. В этом случае получаем алгоритм наискорейшего спуска.
Если λ определяется в результате одномерной минимизации, то
градиент в точке очередного приближения будет ортогонален направлению предыдущего спуска
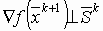 .
.
Вообще говоря, процедура наискорейшего спуска может закончиться в стационарной точке
любого типа, в которой 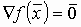 . Поэтому следует проверять, не завершился ли
алгоритм в седловой точке.
. Поэтому следует проверять, не завершился ли
алгоритм в седловой точке.
Эффективность алгоритма зависит от вида минимизируемой функции. Алгоритм наискорейшего
спуска сойдется за одну итерацию при любом начальном приближении для функции
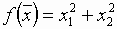 , но сходимость будет очень медленной, например, в случае функции вида
, но сходимость будет очень медленной, например, в случае функции вида
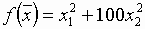 . В тех ситуациях, когда линии уровня минимизируемой функции представляет
собой прямолинейный или, хуже того, криволинейный "овраг" эффективность алгоритма оказывается
очень низкой. Очевидно, что хорошие результаты может давать предварительное масштабирование
функций.
. В тех ситуациях, когда линии уровня минимизируемой функции представляет
собой прямолинейный или, хуже того, криволинейный "овраг" эффективность алгоритма оказывается
очень низкой. Очевидно, что хорошие результаты может давать предварительное масштабирование
функций.
Процесс наискорейшего спуска обычно быстро сходится вдали от точки экстремума и медленно в районе экстремума. Поэтому метод наискорейшего спуска нередко используют в комбинации с другими алгоритмами.
В алгоритме наискорейшего спуска на каждом этапе поиска используется только текущая
информация о функции 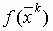 и градиенте
и градиенте 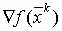 .
В алгоритмах сопряженных градиентов используется информация о поиске на предыдущих
этапах спуска.
.
В алгоритмах сопряженных градиентов используется информация о поиске на предыдущих
этапах спуска.
Направление поиска на текущем шаге 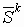 строится как линейная комбинация
наискорейшего спуска на данном шаге
строится как линейная комбинация
наискорейшего спуска на данном шаге 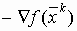 и направлений спуска на предыдущих
шагах
и направлений спуска на предыдущих
шагах 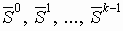 . Веса в линейной комбинации выбираются таким образом, чтобы
сделать эти направления сопряженными. В этом случае квадратичная функция будет минимизироваться
за шаг алгоритма.
. Веса в линейной комбинации выбираются таким образом, чтобы
сделать эти направления сопряженными. В этом случае квадратичная функция будет минимизироваться
за шаг алгоритма.
При выборе весов используется только текущий градиент и градиент в предыдущей точке.
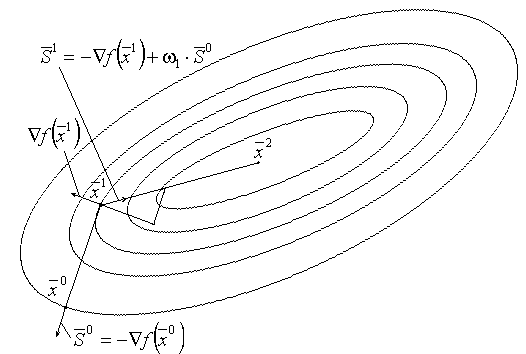
В начальной точке 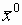 направление спуска
направление спуска 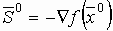 :
:
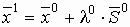 , где λ0 выбирается из соображений минимальности целевой функции
в данном направлении
, где λ0 выбирается из соображений минимальности целевой функции
в данном направлении 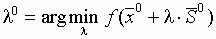 . Новое направление поиска
. Новое направление поиска 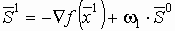 , где
ω1 выбирается так, чтобы сделать направления
, где
ω1 выбирается так, чтобы сделать направления 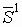 и
и
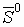 сопряженными по отношению к матрице H:
сопряженными по отношению к матрице H: 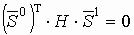 . (*)
. (*)
Для квадратичной функции справедливы соотношения: 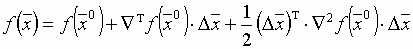 , где
, где 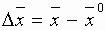 ,
,
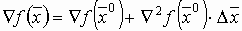 .
.
Если положить 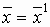 , тогда
, тогда 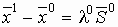 и
и 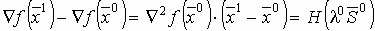 .
.
Воспользуемся последним выражением, чтобы исключить 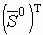 из уравнения (*).
Для квадратичной функции H = HT, поэтому
из уравнения (*).
Для квадратичной функции H = HT, поэтому 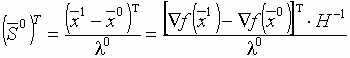 .
.
Следовательно, для сопряженности 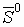 и
и 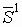 :
:
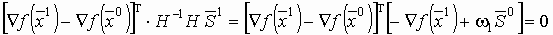 .
.
Вследствие изложенных ранее свойств сопряженности все перекрестные члены исчезают.
Учитывая, что 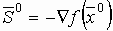 , получим для ω1 следующее
соотношение:
, получим для ω1 следующее
соотношение: 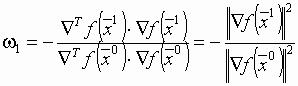 .
.
Направление поиска 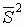 строится в виде линейной комбинации векторов
строится в виде линейной комбинации векторов
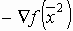 ,
, 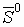 ,
, 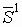 , причем так,
чтобы оно было сопряженным с
, причем так,
чтобы оно было сопряженным с 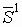 . Если распространить сделанные
выкладки на
. Если распространить сделанные
выкладки на 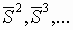 , опуская их содержание и учитывая, что
, опуская их содержание и учитывая, что 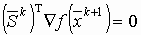 приводит к
приводит к 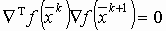 , можно получить общее выражение для ωk:
, можно получить общее выражение для ωk:
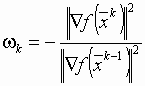 (**).
(**).
Все весовые коэффициенты, предшествующие ωk, что особенно интересно, оказываются нулевыми.
Полностью алгоритм описывается следующей последовательностью действий:
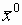 вычисляется
вычисляется 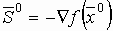 .
.
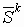 определяется минимум функции, то есть решается задача
определяется минимум функции, то есть решается задача 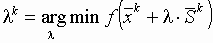 и находится
первое приближение
и находится
первое приближение 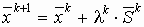 .
.
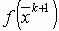 и
и 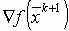 .
.
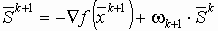 .
.
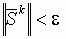 , где ε –
заданная величина.
, где ε –
заданная величина.
 на
на
 и возвратом на первый пункт алгоритма.
и возвратом на первый пункт алгоритма.
Если исходная функция является квадратичной, то (n+1)-е приближение даст точку экстремума данной функции. Описанный алгоритм с построением ωk по формулам (**) соответствует методу сопряженных градиентов Флетчера-Ривса.
В модификации Полака-Рибьера (Пшеничного) метод сопряженных градиентов
отличается только вычислением 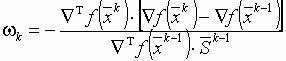 .
.
В случае квадратичных функций обе модификации примерно эквивалентны, однако в модификации Полака-Рибьера алгоритм обычно оказывается несколько эффективнее.
Милем и Кентреллом предложен метод поиска, основанный на использовании двух подбираемых
параметров для минимизации  в каждом направлении поиска. В этом
алгоритме последовательность действий определяется формулой:
в каждом направлении поиска. В этом
алгоритме последовательность действий определяется формулой: 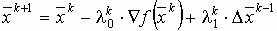 , где
, где 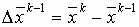 .
.
На каждом шаге решается задача минимизации по двум параметрам: 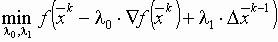 .
.
После чего находится очередное приближение. При этом можно показать, что 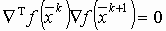 ,
,
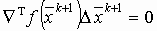 и
и 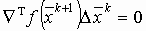 .
.
На первом шаге 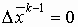 , а
, а 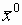 должно быть задано. На
k-м шаге:
должно быть задано. На
k-м шаге:
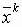 ,
, 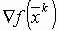 и
и 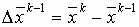 .
.
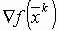 и
и 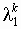 .
.
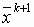 и переходят к пункту 1.
и переходят к пункту 1.
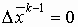 .
.
Процесс заканчивается, когда 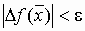 .
.
На квадратичных функциях алгоритм по эффективности близок к методу сопряженных градиентов.
Крэгг и Леви распространили данный метод на случай большего числа параметров. На каждом шаге
при минимизации 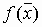 в заданном направлении решается задача вида
в заданном направлении решается задача вида
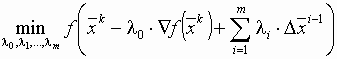 , а очередное приближение
, а очередное приближение 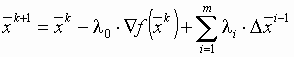 при m ≤ n - 1.
при m ≤ n - 1.
Достоинства и недостатки такого подхода очевидны.