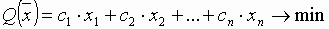 ,
,
Метод предназначен для решения общей задачи линейного программирования.
Пусть имеем следующую задачу:
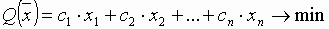 ,
,
с системой ограничений следующего вида:
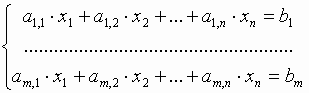 .
.
Разрешим эту систему относительно переменных x1, ...,xm:
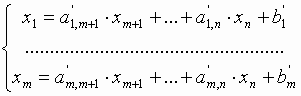 .
.
Векторы условий, соответствующие x1, ...,xm, образуют базис. Переменные x1, ...,xm назовем базисными переменными. Остальные переменные задачи – небазисные.
Целевую функцию можно выразить через небазисные переменные:
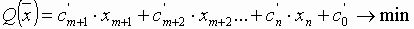 .
.
Если приравнять небазисные переменные нулю: xm+1 = 0, xm+2 = 0, ..., xn = 0,
то соответствующие базисные переменные примут значения: 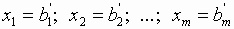 .
.
Вектор 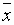 с такими компонентами представляет собой угловую
точку многогранника решений (допустимую) при условии, что
с такими компонентами представляет собой угловую
точку многогранника решений (допустимую) при условии, что 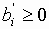 (опорный план).
(опорный план).
Теперь необходимо перейти к другой угловой точке с меньшим значением целевой функции. Для этого следует выбрать некоторую небазисную переменную и некоторую базисную так, чтобы после того, как мы “поменяем их местами”, значение целевой функции уменьшилось. Такой направленный перебор в конце концов приведет нас к решению задачи.
Пусть 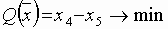
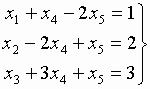 .
.
Выберем в качестве базисных следующие переменные {x1, x2, x3} и разрешим систему относительно этих переменных. Система ограничений примет следующий вид:
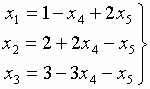 .
.
Переменные {x4, x5}являются небазисными.
Если взять x4 = 0 и x5 = 0, то получим угловую точку
(опорный план): 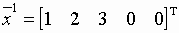 , которому соответствует
, которому соответствует 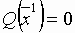 .
.
Значение целевой функции можно уменьшить за счет увеличения x5. При увеличении x5 величина x1 также увеличивается, а x2 и x3 – уменьшаются. Причем величина x2 раньше может стать отрицательной. Поэтому, вводя в базис переменную x5, одновременно x2 исключаем из базиса. В результате после очевидных преобразований получим следующие выражения для новой системы базисных переменных и целевой функции:
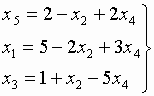
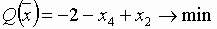 .
.
Соответствующий опорный план: 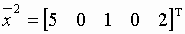 и
и 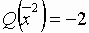 .
.
Целевую функцию можно уменьшить за счет увеличения x4. Увеличение x4 приводит к уменьшению только x3. Поэтому вводим в базис переменную x4, а x3 исключаем из базиса. В результате получим следующие выражения для новой системы базисных переменных и целевой функции:
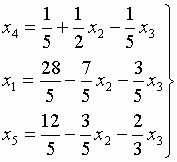
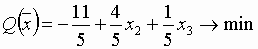 .
.
Соответствующий опорный план: 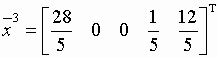 и значение целевой функции:
и значение целевой функции: 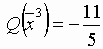 . Так как все коэффициенты при
небазисных переменных в целевой функции неотрицательны, то нельзя уменьшить
целевую функцию за счет увеличения x2 или x3,
следовательно, полученный план
. Так как все коэффициенты при
небазисных переменных в целевой функции неотрицательны, то нельзя уменьшить
целевую функцию за счет увеличения x2 или x3,
следовательно, полученный план 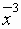 является оптимальным.
является оптимальным.
Пусть имеем задачу
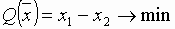
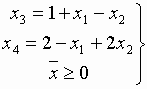 .
.
Переменные {x3, x4}- базисные, а
{x1, x2}- небазисные переменные. Опорный план
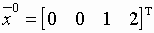 ,
, 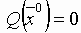 .
.
Теперь вводим в базис переменную x1, a x4 исключаем из базиса. В результате получим следующие выражения для базисных переменных и целевой функции:
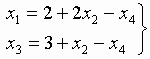
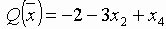 .
.
Опорный план: 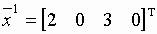 , значение целевой функции:
, значение целевой функции:
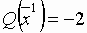 .
.
Теперь можно заметить, что при увеличении x2 значения переменных
x1 и x3 также возрастают, то есть при
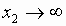 в допустимой области
в допустимой области 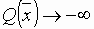 (задача не имеет решения).
(задача не имеет решения).
В процессе поиска допустимого плана может быть выявлена противоречивость системы ограничений.
Формализованный алгоритм симплекс метода состоит из двух основных этапов:
Проиллюстрируем алгоритм на рассмотренном ранее примере:
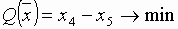
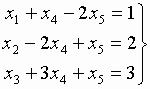 .
.
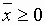 .
.
В случае базисных переменных {x1, x2, x3}начальная симплексная таблица для данного примера будет выглядеть следующим образом:
| -x4 | -x5 | 1 | |
| x1= | 1 | -2 | 1 |
| x2= | -2 | 1 | 2 |
| x3= | 3 | 1 | 3 |
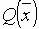 = = |
-1 | 1 | 0 |
Она уже соответствует опорному плану 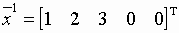 (столбец свободных членов).
(столбец свободных членов).
Для того чтобы опорный план был оптимален, при минимизации целевой
функции необходимо, чтобы коэффициенты в строке целевой функции были
неположительными (в случае максимизации – неотрицательными). Т.е. при
поиске минимума мы должны освободиться от положительных коэффициентов в
строке 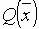 .
.
Выбор разрешающего элемента. Если при поиске минимума в строке целевой функции есть коэффициенты больше нуля, то выбираем столбец с положительным коэффициентом в строке целевой функции в качестве разрешающего. Пусть это столбец с номером l.
Для выбора разрешающей строки (разрешающего элемента) среди положительных коэффициентов разрешающего столбца выбираем тот (строку), для которого отношение коэффициента в столбце свободных членов к коэффициенту в разрешающем столбце минимально:
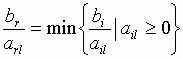 .
.
arl – разрешающий (направляющий) элемент, строка r – разрешающая.
Для перехода к следующей симплексной таблице (следующему опорному плану с меньшим значением целевой функции) делается шаг модифицированного жорданова исключения с разрешающим элементом arl.
Если в разрешающем столбце нет положительных коэффициентов, то целевая функция неограничена снизу (при максимизации – неограничена сверху).
Шаг модифицированного жорданова исключения над симплексной таблицей. На месте разрешающего элемента ставится 1 и делится на разрешающий элемент.
Остальные элементы разрешающего столбца меняют знак на противоположный и делятся на разрешающий элемент.
Остальные элементы разрешающей строки делятся на разрешающий элемент.
Все остальные элементы симплексной таблицы вычисляются по следующей формуле:
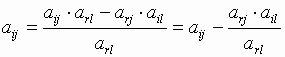 .
.
|
|
|
Пусть необходимо решить задачу:
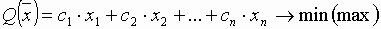
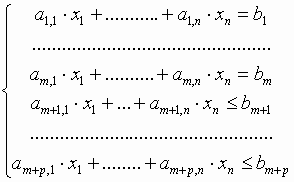 .
.
Введем дополнительные переменные, чтобы преобразовать ограничения-неравенства к равенствам. В ограничениях-равенствах дополнительные переменные должны быть нулевыми. Тогда система ограничений принимает вид:
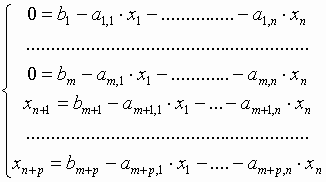 ,
,
где xn + i ≥ 0, i = 1, ..., p.
В качестве базисных переменных будем брать систему дополнительно введенных переменных. Тогда симплексная таблица для преобразованной задачи будет иметь следующий вид:
| -x1 | -x2 | …. | -xs | .… | -xn | 1 | |
| 0 | a1,1 | a1,2 | …. | a1,s | …. | a1,n | b1 |
| …. | …. | …. | …. | …. | …. | …. | …. |
| 0 | am,1 | am,2 | …. | am,s | …. | am,n | bm |
| xm+1 | am+1,1 | am+1,2 | …. | am+1,s | …. | am+1,n | bm+1 |
| …. | …. | …. | …. | …. | …. | …. | …. |
| xm+p | am+p,1 | am+p,2 | …. | am+p,s | …. | am+p,n | bm+p |
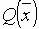 |
-c1 | -c2 | …. | -cs | …. | -cn | 0 |
Правила выбора разрешающего элемента при поиске опорного плана.
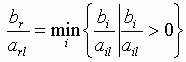 , где r - номер
разрешающей строки. Таким образом, arl - разрешающий элемент.
, где r - номер
разрешающей строки. Таким образом, arl - разрешающий элемент.
Рассматривая симплекс-метод, мы предполагали, что задача линейного программирования является невырожденной, т.е. каждый опорный план содержит ровно m положительных компонент, где m – число ограничений в задаче. В вырожденном опорном плане число положительных компонент оказывается меньше числа ограничений: некоторые базисные переменные, соответствующие данному опорному плану, принимают нулевые значения. Используя геометрическую интерпретацию для простейшего случая, когда n - m = 2 (число небазисных переменных равно 2), легко отличить вырожденную задачу от невырожденной. В вырожденной задаче в одной вершине многогранника условий пересекается более двух прямых, описываемых уравнениями вида xi = 0. Это значит, что одна или несколько сторон многоугольника условий стягиваются в точку.
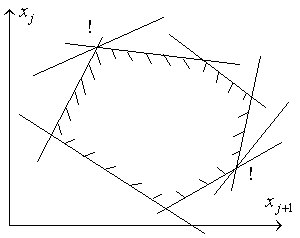
Аналогично при n - m = 3 в вырожденной задаче в одной вершине пересекается более 3-х плоскостей xi = 0.
В предположении о невырожденности задачи находилось только одно значение
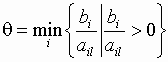 , по которому определялся индекс выводимого из базиса вектора
условий (выводимой из числа базисных переменной). В вырожденной задаче
, по которому определялся индекс выводимого из базиса вектора
условий (выводимой из числа базисных переменной). В вырожденной задаче
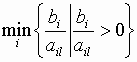 может достигаться на нескольких индексах сразу
(для нескольких строк). В этом случае в находимом опорном плане несколько базисных
переменных будут нулевыми.
может достигаться на нескольких индексах сразу
(для нескольких строк). В этом случае в находимом опорном плане несколько базисных
переменных будут нулевыми.
Если задача линейного программирования оказывается вырожденной, то при плохом выборе вектора условий, выводимого из базиса, может возникнуть бесконечное движение по базисам одного и того же опорного плана. Так называемое, явление зацикливания. Хотя в практических задачах линейного программирования зацикливание явление крайне редкое, возможность его не исключена.
Один из приемов борьбы с вырожденностью состоит в преобразовании задачи путем "незначительного" изменения вектора правых частей системы ограничений на величины εi, таким образом, чтобы задача стала невырожденной, и, в то же время, чтобы это изменение не повлияло реально на оптимальный план задачи.
Чаще реализуемые алгоритмы включают в себя некоторые простые правила, снижающие вероятность возникновения зацикливания или его преодоления.
Пусть переменную xj необходимо сделать базисной.
Рассмотрим множество индексов E0, состоящее из тех i,
для которых достигается 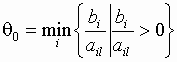 . Множество индексов i,
для которых выполняется данное условие обозначим через E0.
Если E0 состоит из одного элемента, то из базиса исключается вектор
условий Ai (переменная xi делается небазисной).
Если E0 состоит более чем из одного элемента, то составляется множество
E1, которое состоит из
. Множество индексов i,
для которых выполняется данное условие обозначим через E0.
Если E0 состоит из одного элемента, то из базиса исключается вектор
условий Ai (переменная xi делается небазисной).
Если E0 состоит более чем из одного элемента, то составляется множество
E1, которое состоит из 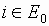 , на которых
достигается
, на которых
достигается 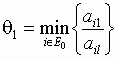 . Если E1 состоит из одного индекса
k, то из базиса выводится переменная xk. В противном случае
составляется множество E2 и т.д.
. Если E1 состоит из одного индекса
k, то из базиса выводится переменная xk. В противном случае
составляется множество E2 и т.д.
Практически правилом надо пользоваться, если зацикливание уже обнаружено.