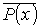Логические операции над предикатами

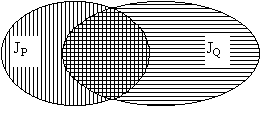
Конъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x) & Q(x), который принимает значение И для тех и только тех значений x из множества M, при которых каждый из предикатов принимает значение И, и принимает значение Л во всех остальных случаях.

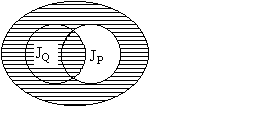
Областью истинности предиката P(x) & Q(x) является пересечение множеств J_P ∩ J_Q.

Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат P(x) V Q(x), который принимает значение Л для тех и только тех значений x из множества M, при которых каждый из предикатов принимает значение Л, и принимает значение И во всех остальных случаях.

Областью истинности предиката P(x) V Q(x) является объединение множеств J_P U J_Q.

Отрицанием предиката P(x) называется новый предикат 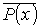, который принимает значение И при всех тех значениях x из множества M, при которых предикат P(x) принимает значение Л, и принимает значение Л при всех тех значениях x из множества M, при которых предикат P(x) принимает значение И.

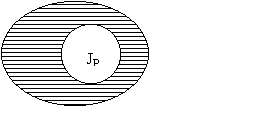
Областью истинности предиката 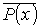является дополнение множества J_P до множества М.

Импликацией предикатов P(x) и Q(x) называется новый предикат P(x) → Q(x), который принимает значение Л для тех и только тех значений x из множества M, при которых одновременно предикат P(x) принимает значение И, а Q(x) - значение Л и принимает значение И во всех остальных случаях.

Так как при каждом фиксированном x из М справедлив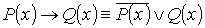о , то .

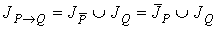Принято считать, что связки Þ и Û связывают слабее, чем & и V.

Назад