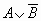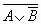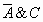1. Составим таблицу истинности для формулы 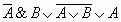 , которая содержит
две переменные A и B. В первых двух столбцах
таблицы запишем четыре возможных пары значений этих переменных, в последующих
столбцах — значения промежуточных формул и в последнем столбце — значение
формулы. В результате получим таблицу:
, которая содержит
две переменные A и B. В первых двух столбцах
таблицы запишем четыре возможных пары значений этих переменных, в последующих
столбцах — значения промежуточных формул и в последнем столбце — значение
формулы. В результате получим таблицу:
| Переменные |
Промежуточные логические формулы |
Формула |
| A |
B |
Ā |
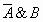 |
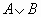 |
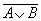 |
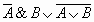 |
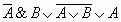 |
| Л | Л | И | Л |
Л | И | И | И |
| Л | И | И | И |
И | Л | И | И |
| И | Л | Л | Л |
И | Л | Л | И |
| И | И | Л | Л |
И | Л | Л | И |
Из таблицы видно, что при всех наборах значений переменных A и B формула
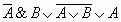 принимает значение И, то есть является тождественно истинной.
принимает значение И, то есть является тождественно истинной.
2. Таблица истинности для формулы 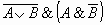 :
:
| Переменные |
Промежуточные логические формулы |
Формула |
| A |
B |
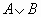 |
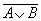 |
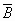 |
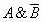 |
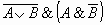 |
| Л | Л | Л | И |
И | Л | Л |
| Л | И | И | Л |
Л | Л | Л |
| И | Л | И | Л |
И | И | Л |
| И | И | И | Л |
Л | Л | Л |
Из таблицы видно, что при всех наборах значений переменных A и B
формула 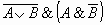 принимает значение Л, то есть является тождественно
ложной.
принимает значение Л, то есть является тождественно
ложной.
3. Таблица истинности для формулы 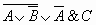 :
:
| Переменные |
Промежуточные логические формулы |
Формула |
| A |
B |
C |
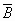 |
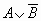 |
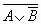 |
Ā |
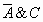 |
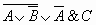 |
| Л | Л | Л | И | И |
Л | И | Л | Л |
| Л | Л | И | И | И |
Л | И | И | И |
| Л | И | Л | Л | Л |
И | И | Л | И |
| Л | И | И | Л | Л |
И | И | И | И |
| И | Л | Л | И | И |
Л | Л | Л | Л |
| И | Л | И | И | И |
Л | Л | Л | Л |
| И | И | Л | Л | И |
Л | Л | Л | Л |
| И | И | И | Л | И |
Л | Л | Л | Л |
Из таблицы видно, что формула 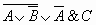 в
некоторых случаях принимает значение И, а в некоторых — Л, то есть является
выполнимой.
в
некоторых случаях принимает значение И, а в некоторых — Л, то есть является
выполнимой.
Назад
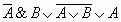 , которая содержит
две переменные A и B. В первых двух столбцах
таблицы запишем четыре возможных пары значений этих переменных, в последующих
столбцах — значения промежуточных формул и в последнем столбце — значение
формулы. В результате получим таблицу:
, которая содержит
две переменные A и B. В первых двух столбцах
таблицы запишем четыре возможных пары значений этих переменных, в последующих
столбцах — значения промежуточных формул и в последнем столбце — значение
формулы. В результате получим таблицу: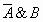
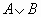
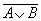
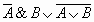
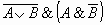 :
: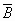
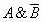
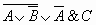 :
: