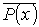Методы перевода с естественного языка на математический и обратно

Теоретические сведения

В классической логике большое внимание уделяется четырем типам категорических высказываний (так называемые ограниченные кванторы). Обычно они обозначаются так:

A - общеутвердительное высказывание "Всякое S есть Р": "x (S(x) ÞP(x))

Е - общеотрицательное высказывание "Никакое S не есть P": "x (S(x) Þ )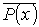

I - частноутвердительное высказывание "Некоторые S есть Р": $x (S(x) & P(x))

О - частноотрицательное высказывание "Некоторые S не есть Р": $x (S(x) & )

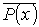Если на значения переменной накладываются сразу несколько ограничений, то все они перечисляются через &, а затем надстраивается ограниченный квантор по обычным правилам.

Логическую формулу, являющуюся переводом предложения естественного языка, чаще всего лучше составлять изнутри, начиная с середины, а не сначала, как пишут обычные предложения.

При переводе с формального языка на естественный утверждений с вложенными кванторами необходимо тщательно следить за порядком кванторов и областью их действия.

Прочитав утверждение, следует, по возможности, сформулировать полученное предложение более кратно, более выразительно.

Свободные переменные должны входить в окончательную словесную формулировку.

Во многих предложениях корректный перевод на формальный язык невозможен без учета контекста.