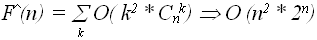Теоретический предел трудоемкости задачи
Рассматривая некоторую алгоритмически разрешимую задачу, и анализируя один
из алгоритмов ее решения, мы можем получить оценку трудоемкости этого
алгоритма в худшем случае – fa( )=O(g(
)=O(g( )). Такие же оценки
мы можем получить и для других известных алгоритмов решения данной задачи.
Рассматривая задачу с этой точки зрения, возникает резонный вопрос – а
существует ли функциональный нижний предел для g(
)). Такие же оценки
мы можем получить и для других известных алгоритмов решения данной задачи.
Рассматривая задачу с этой точки зрения, возникает резонный вопрос – а
существует ли функциональный нижний предел для g( ) и если «да», то существует ли алгоритм,
решающий задачу с такой трудоемкостью в худшем случае.
) и если «да», то существует ли алгоритм,
решающий задачу с такой трудоемкостью в худшем случае.
Другая, более точная формулировка, имеет следующий вид: какова оценка сложности самого «быстрого» алгоритма решения данной задачи в худшем случае? Очевидно, что это оценка самой задачи, а не какого либо алгоритма ее решения. Таким образом, мы приходим к определению понятия функционального теоретического нижнего предела трудоемкости задачи в худшем случае:
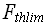 = min {
= min {  (
(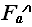 (D)) }
(D)) }
Если мы можем на основе теоретических рассуждений доказать существование и
получить оценивающую функцию, то мы можем утверждать, что любой алгоритм,
решающий данную задачу работает не быстрее, чем с оценкой 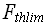 в худшем случае:
в худшем случае:
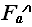 (D) =
(D) = 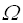 (
(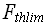 )
)
- Приведем ряд примеров:
-
Задача поиска максимума в массиве A=(a1,…,an) – для этой задачи, очевидно должны быть просмотрены все элементы, и
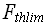 =
= 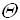 (n).
(n). -
Задача умножения матриц - для этой задачи можно сделать предположение, что необходимо выполнить некоторые арифметические операции со всеми исходными данными, теоретическое обоснование какой–либо другой оценки на сегодня не известно, что приводит нас к оценке
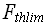 =Q (
=Q (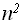 ). Отметим, что лучший алгоритм умножения матриц имеет оценку Q
(
). Отметим, что лучший алгоритм умножения матриц имеет оценку Q
(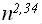 ). Расхождение между
теоретическим пределом и оценкой лучшего известного алгоритма позволяет
предположить, что либо существует, но еще не найден более быстрый алгоритм
умножения матриц, либо оценка Q (
). Расхождение между
теоретическим пределом и оценкой лучшего известного алгоритма позволяет
предположить, что либо существует, но еще не найден более быстрый алгоритм
умножения матриц, либо оценка Q (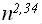 ) должна быть доказана, как теоретический предел.
) должна быть доказана, как теоретический предел.
Сложностные классы задач
В начале 1960-х годов, в связи с началом широкого использования вычислительной техники для решения практических задач, возник вопрос о границах практической применимости данного алгоритма решения задачи в смысле ограничений на ее размерность. Какие задачи могут быть решены на ЭВМ за реальное время?
Ответ на этот вопрос был дан в работах Кобмена (Alan Cobham, 1964), и Эдмнодса (Jack Edmonds, 1965), где были введены сложностные классы задач.
1) Класс P (задачи с полиномиальной сложностью)
Задача называется полиномиальной, т.е. относится к классу P, если
существует константа k и алгоритм, решающий задачу с 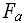 (n)=O(
(n)=O(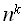 ), где n - длина входа алгоритма в битах n = |D| [6].
), где n - длина входа алгоритма в битах n = |D| [6].
Задачи класса P – это интуитивно, задачи, решаемые за реальное время.
- Отметим следующие преимущества
алгоритмов из этого класса:
-
для большинства задач из класса P константа k меньше 6;
-
класс P инвариантен по модели вычислений (для широкого класса моделей);
-
класс P обладает свойством естественной замкнутости (сумма или произведение полиномов есть полином).
Таким образом, задачи класса P есть уточнение определения «практически разрешимой» задачи.
2) Класс NP (полиномиально проверяемые задачи)
Представим себе, что некоторый алгоритм получает решение некоторой задачи – соответствует ли полученный ответ поставленной задаче, и насколько быстро мы можем проверить его правильность?
Рассмотрим, например задачу о сумме:
Дано N чисел – А = (a1,…an) и число V.
Задача: Найти вектор (массив) X=(x1,…,xn), xiє{0,1}, такой, что 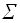 aixi = V.
aixi = V.
Содержательно: может ли быть представлено число V в виде суммы каких-либо элементов массива А.
Если какой-то алгоритм выдает результат – массив X, то проверка
правильности этого результата может быть выполнена с полиномиальной
сложно-стью: проверка 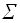 aixi = V
требует не более Q (N) операций.
aixi = V
требует не более Q (N) операций.
Формально: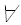 Dє
Dє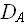 , |D|=n поставим в соответствие сертификат
Sє
, |D|=n поставим в соответствие сертификат
Sє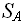 , такой что |S|=O (
, такой что |S|=O (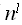 ) и алгоритм
) и алгоритм 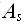 =
= 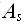 (D,S), такой, что он
выдает «1», если решение правильно, и «0», если решение неверно. Тогда задача
принадлежит классу NP, если F (
(D,S), такой, что он
выдает «1», если решение правильно, и «0», если решение неверно. Тогда задача
принадлежит классу NP, если F ( 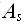 )=O (
)=O ( 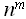 ).
).
Содержательно задача относится к классу NP, если ее решение некоторым алгоритмом может быть быстро (полиномиально) проверено.
Проблема P = NP
После введения в теорию алгоритмов понятий сложностных классов Эдмондсом (Edmonds, 1965) была поставлена основная проблема теории сложности – P = NP ? Словесная формулировка проблемы имеет вид: можно ли все задачи, решение которых проверяется с полиномиальной сложностью, решить за полиномиальное время ?
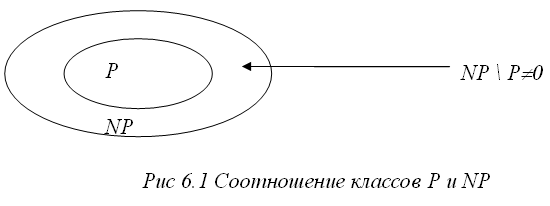
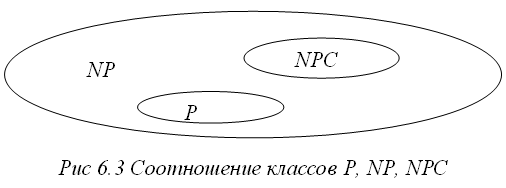
Очевидно, что любая задача, принадлежащая классу P, принадлежит и классу NP, т.к. она может быть полиномиально проверена – задача проверки решения может состоять просто в повторном решении задачи.
На сегодня отсутствуют теоретические доказательства как совпадения этих классов (P=NP), так и их несовпадения. Предположение состоит в том, что класс P является собственным подмножеством класса NP, т.е. NP \ P не пусто – рис 6.1
Класс NPC (NP – полные задачи)
Понятие NP – полноты было введено независимо Куком (Stephen Cook, 1971) и Левиным (журнал «Проблемы передачи информации», 1973,т.9, вып. 3) и основывается на понятии сводимости одной задачи к другой.
Сводимость может быть представлена следующим образом: если мы имеем задачу 1 и решающий эту задачу алгоритм, выдающий правильный ответ для всех конкретных проблем, составляющих задачу, а для задачи 2 алгоритм решения неизвестен, то если мы можем переформулировать (свести) задачу 2 в терминах задачи 1, то мы решаем задачу 2.
Таким образом, если задача 1 задана множеством конкретных проблем 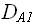 , а задача 2 – множеством, и
существует функция
, а задача 2 – множеством, и
существует функция 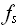 (алгоритм),
сводящая конкретную постановку задачи 2 (
(алгоритм),
сводящая конкретную постановку задачи 2 ( 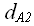 ) к конкретной постановке задачи 1(
) к конкретной постановке задачи 1(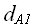 ):
): 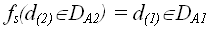 , то задача 2
сводима к задаче 1.
, то задача 2
сводима к задаче 1.
Если при этом 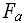 (
(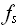 ) = O(
) = O(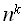 ), т.е. алгоритм сведения принадлежит классу P, то говорят, что
задача 1 полиномиально сводится к задаче 2.
), т.е. алгоритм сведения принадлежит классу P, то говорят, что
задача 1 полиномиально сводится к задаче 2.
Принято говорить, что задача задается некоторым языком, тогда если задача 1 задана языком L1, а задача 2 – языком L2, то полиномиальная сводимость обозначается следующим образом: L2 =< pL1.
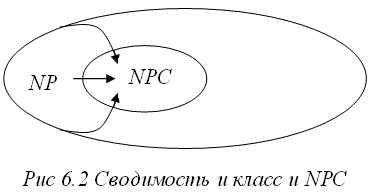
Определение класса NPC (NP-complete) или класса NP-полных задач требует выполнения следующих двух условий: во-первых, задача должна принадлежать классу NP (L є NP), и, во-вторых, к ней полиномиально должны сводиться все задачи из класса NP (Lx=< pL, для каждого Lx є NP), что схематично представлено на рис 6.2.
Для класса NPC доказана следующая теорема: Если существует задача,
принадлежащая классу NPC, для которой существует полиномиальный алгоритм
решения (F = O(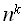 )), то класс P
совпадает с классом NP, т.е. P=NP.
)), то класс P
совпадает с классом NP, т.е. P=NP.
Схема доказательства состоит в сведении любой задачи из NP к данной задаче из класса NPC с полиномиальной трудоемкостью и решении этой задачи за полиномиальное время (по условию теоремы).
В настоящее время доказано существование сотен NP–полных задач, но ни для
одной из них пока не удалось найти полиномиального алгоритма решения. В
настоящее время исследователи предполагают следующее соотношение классов,
показанное на рис 6.3 – P 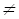 NP,
то есть NP \ P
NP,
то есть NP \ P 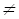 0, и задачи из
класса NPC не могут быть решены (сегодня) с полиномиальной
трудоемкостью.
0, и задачи из
класса NPC не могут быть решены (сегодня) с полиномиальной
трудоемкостью.
Примеры NP – полных задач
1 Задача о выполнимости схемы
Рассмотрим схему из функциональных элементов «и», «или», «не» с n битовыми
входами и одним выходом, состоящую не более, чем из O(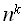 ) элементов – рис 6.4
) элементов – рис 6.4
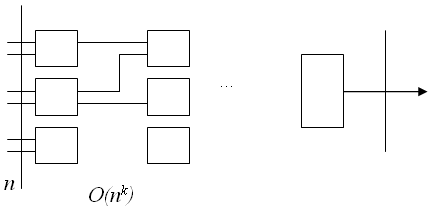
Будем понимать под выполняющим набором значений из множества {0,1} на входе схемы, такой набор входов – значения x1,…,xn, при котором на выходе схемы будет значение «1».
Формулировка задачи – существует ли для данной схемы выполняющий набор
значений входа. Очевидно, что задача принадлежит классу NP – проверка
предъявленного выполняющего набора не сложнее количества функциональных
элементов, и следовательно не больше чем O(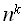 ).
).
Это была одна из первых задач, для которой была доказана ее NP полнота, т.е. любая задача из класса NP полиномиально сводима к задаче о выполнимости схемы.
Решение этой задачи может быть получено перебором всех 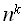 возможных значений входа с последующей
проверкой на соответствие условию выполняющего набора. В худшем случае
придется проверить все возможные значения входа, что приводит к оценке
возможных значений входа с последующей
проверкой на соответствие условию выполняющего набора. В худшем случае
придется проверить все возможные значения входа, что приводит к оценке 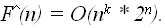 Для этой, как и для всех других
NP–полных задач не известен полиномиальный алгоритм решения.
Для этой, как и для всех других
NP–полных задач не известен полиномиальный алгоритм решения.
2 Задача о сумме
Уже рассмотренная задача о сумме также является NP–полной, отметим, что если количество слагаемых фиксировано, то сложность задачи является полиномиальной, так как:
-
для 2-х слагаемых
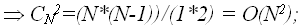
-
для 3-х слагаемых
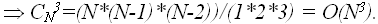
Однако в общем случае придется перебирать 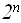 различных вариантов, так как по биномиальной теореме
различных вариантов, так как по биномиальной теореме 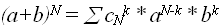 , а при a=b=1, имеем:
, а при a=b=1, имеем: 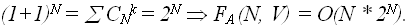
3 Задача о клике
Пусть дан граф G = G(V,E), где V – множество из n вершин, а E – множество ребер. Будем понимать под кликой максимальный по количеству вершин полный подграф в графе в G.
Задача состоит в определении клики в заданном графе G
Поскольку в полном графе на m вершинах имеется m(m-1)/2 ребер, то проверка,
является ли данный граф полным, имеет сложность O (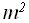 ). Очевидно, что если мы рассматриваем подграф с
m вершинами в графе G с вершинами (m < n), то всего существует
). Очевидно, что если мы рассматриваем подграф с
m вершинами в графе G с вершинами (m < n), то всего существует 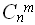 различных подграфов. Если в задаче о клике
количество вершин клики фиксировано, то перебирающий алгоритм имеет
полиномиальную сложность:
различных подграфов. Если в задаче о клике
количество вершин клики фиксировано, то перебирающий алгоритм имеет
полиномиальную сложность:
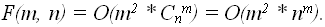
Однако в общем случае придется проверять все подграфы с количеством вершин m = (2, n) на их полноту и определить максимальное значения m для которого в данном графе G существует полный подграф, что приводит к оценке в худшем случае: