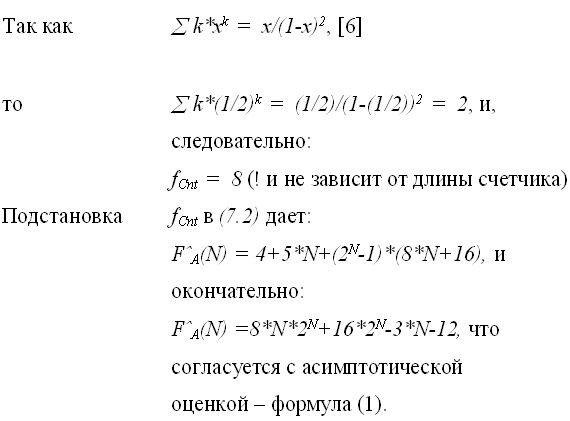Формулировка задачи и асимптотическая оценка
Словесно задача о сумме формулируется как задача нахождения таких чисел из данной совокупности, которые в сумме дают заданное число, классически задача формулируется в терминах целых чисел [6].
В терминах структур данных языка высокого уровня задача формулируется, как задача определения таких элементов исходного массива S из N чисел, которые в сумме дают число V (отметим, что задача относится к классу NPC).
Детальная формулировка:
Дано: Массив S[i], i={1, N} и число
V.
Требуется: определить такие Sj, что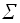 
Sj=V
Тривиальное решение определяется равенством V=Sum, где Sum= 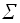Si , условия существования решения имеют
вид:
Min {S[i], i=1,N} =< V =< Sum.
Получим асимптотическую оценку сложности решения данной задачи для алгоритма, использующего прямой перебор всех возможных вариантов. Поскольку исходный массив содержит N чисел, то проверке на равенство V подлежат следующие варианты решений:
-
V содержит 1 слагаемое
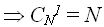вариантов; -
V содержит 2 слагаемых
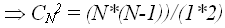вариантов; -
V содержит 3 слагаемых
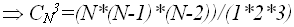вариантов; -
и т.д. до проверки одного варианта с N слагаемыми.
Поскольку сумма биномиальных коэффициентов для степени N равна -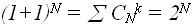 
и для каждого варианта
необходимо выполнить суммирование (с оценкой O(N)) для проверки на V, то
оценка сложности алгоритма в худшем случае имеет вид:
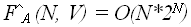(7.1)
Алгоритм точного решения задачи о сумме (метод перебора)
Определим вспомогательный массив, хранящий текущее сочетание исходных чисел в массиве S, подлежащих проверке на V – массив Cnt[j], элемент массива равен «0», если число S[j] не входит в V и равен «1», если число S[j] входит в V
Решение получено, если V =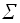S[j]*Cnt[j].
- Могут быть предложены следующие
две реализации механизма полного перебора вариантов:
-
перебор по всевозможным сочетаниям из k элементов по N, т.е. сначала алгоритм пытается представить V как один из элементов массива S, затем перебираются все возможные пары, затем все возможные тройки и т.д.;
-
перебор по двоичному счётчику, реализованному в массиве Cnt: Вторая идея алгоритмически более проста и сводится к решению задаче об увеличении двоичного счётчика в массиве Cnt на «1»:
-
при 00...0111 увеличение на «1» приводит к сбросу всех правых «1» и установке в «1» следующего самого правого «0»;
-
при 00...1000, когда последний элемент счетчика равен «0» увеличение на «1» приводит к переустановке последнего элемента в массиве Cnt с «0» в «1».
Рассматривая массив Cnt как указатель на элементы массива S, подлежащие суммированию в данный момент, мы производим суммирование и проверку на V, до тех пор, пока решение не будет найдено или же безрезультатно будут просмотрены все возможные варианты.
Таким образом, алгоритм точного решения задаче о сумме методом прямого перебора имеет в формальной системе языка высокого уровня следующий вид:
| TASKSUM(S,N,V; CNT,FL) FL <-- false i <-- 1 repeat Cnt[i] <-- 0 i <-- i+1 Until i > N Cnt[N] <-- 1 Repeat Sum <-- 0 i <-- 1 Repeat Sum <-- Sum + S[i] * Cnt[i] |
i <-- i+1 Until i > N if Sum = V FL <-- true Return (Cnt,FL) j <-- N While Cnt[j] = 1 Cnt[j] = 0 j <-- j-1 Cnt[j] <-- 1 Until Cnt[0] = 1 Return(Cnt,FL) |
Анализ алгоритма точного решения задачи о сумме
Рассмотрим лучший и худший случай для данного алгоритма:
-
) В лучшем случае, когда последний элемент массива совпадает со значением V: V=S[N],необходимо выполнить только одно суммирование, что приводит к оценке:
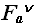(N)=Q(N); -
В худшем случае, если решения вообще нет, то придется проверить все варианты, и
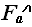(N) = Q (N*
).
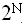Получим детальную оценку для худшего случая, используя принятую методику подсчета элементарных операций:
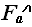(N) = 2+N*(3+2)+2+( 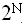-1)*{2+N*(3+5)+1+1+
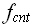+2+2} (7.2)
Для получения значен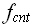ия -
количества операций, необходимых для увеличения счетчика на «1» рассмотрим по
шагам проходы цикла While, в котором выполняется эта операция:
| CNT | Количество проходов в While | Операций |
| 001 | 1 | 6+2 |
| 010 | 0 | 2 |
| 011 | 2 | 2*6+2 |
| 100 | 0 | 2 |
| 101 | 1 | 6+2 |
| 110 | 0 | 2 |
| 111 | 3 | 3*6+2 |
